形如∫dx/(α

来自和讯网https://www.hexun.com/的优秀用户吉禄学阁，于2025-06-28在生活百科知识平台总结分享了一篇关于“形如∫dx/(α-βx)不定积分的计算丘吉尔”的经验，非常感谢吉禄学阁的辛苦付出，他总结的解决技巧方法及常用办法如下：

本例为微积分不定积分计算，积分函数为一次函数倒数形式，并列举当系数均为整数情形、为根式情形和分数情况等不同情况下计算详细过程。

方法/步骤

1/8分步阅读

通用步骤推导：

∫dx/(α-βx)=-∫dx/(βx-α)

=-(1/β)∫dβx/(βx-α)

=-(1/β)∫d(βx-α)/(βx-α)

=-(1/β)ln|βx-α|+C。

[图]2/8

当系数均为整数情形

1.当α=1，β=1情形：

∫dx/(1-x)=-∫dx/(x-1)=-∫d(x-1)/(x-1)=-ln|x-1|+C。

[图]3/8

2.当α=1，β=113情形：

∫dx/(1-113x)=-∫dx/(113x-1)=-(1/113)∫d113x/(113x-1)

=-(1/113)∫d(113x-1)/(113x-1)=-(1/113)ln|113x-1|+C。

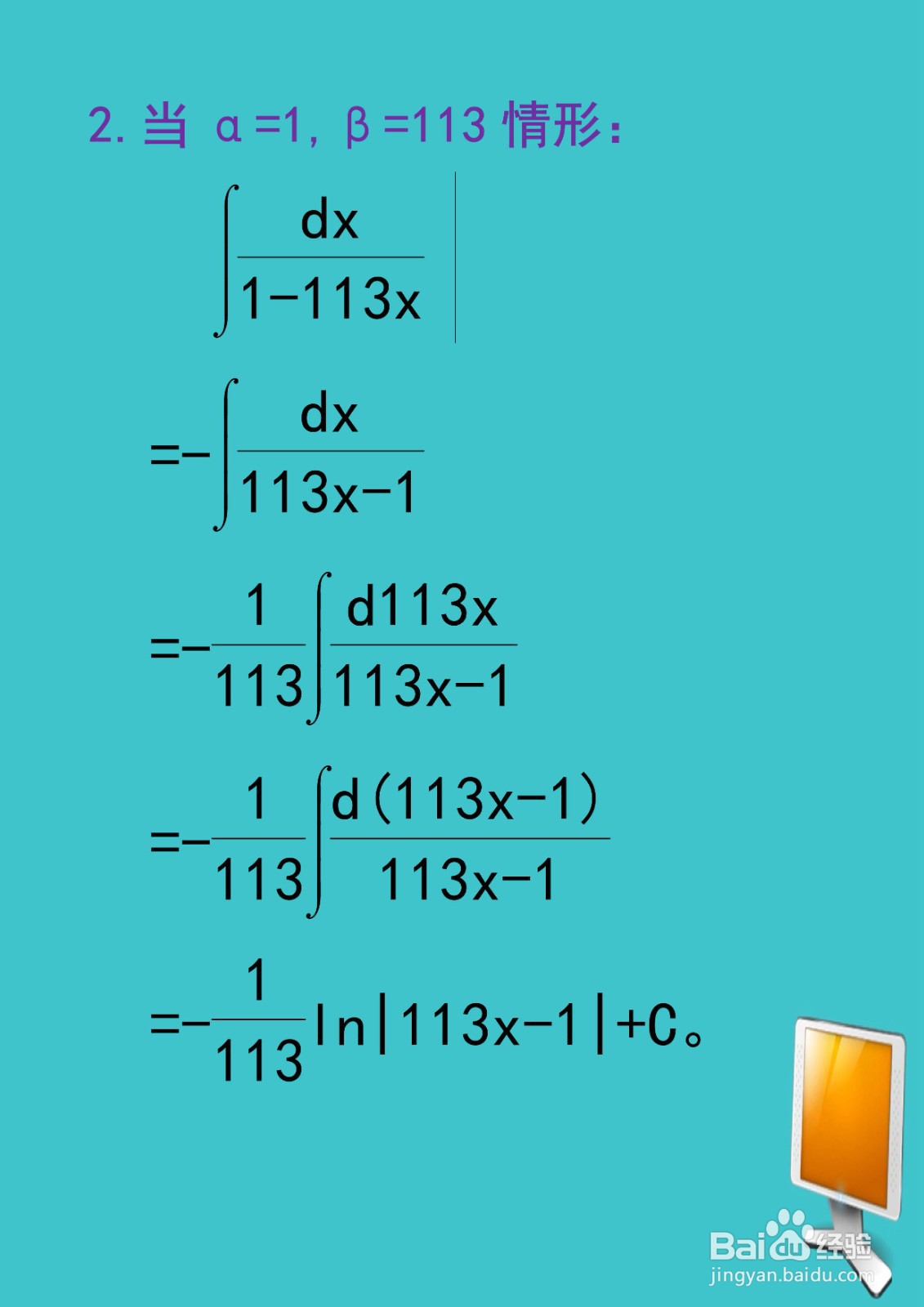[图]4/8

3.当α=288，β=1情形：

∫dx/(288-x)=-∫dx/(x-288)=-∫d(x-288)/(x-288)=-ln|x-288|+C。

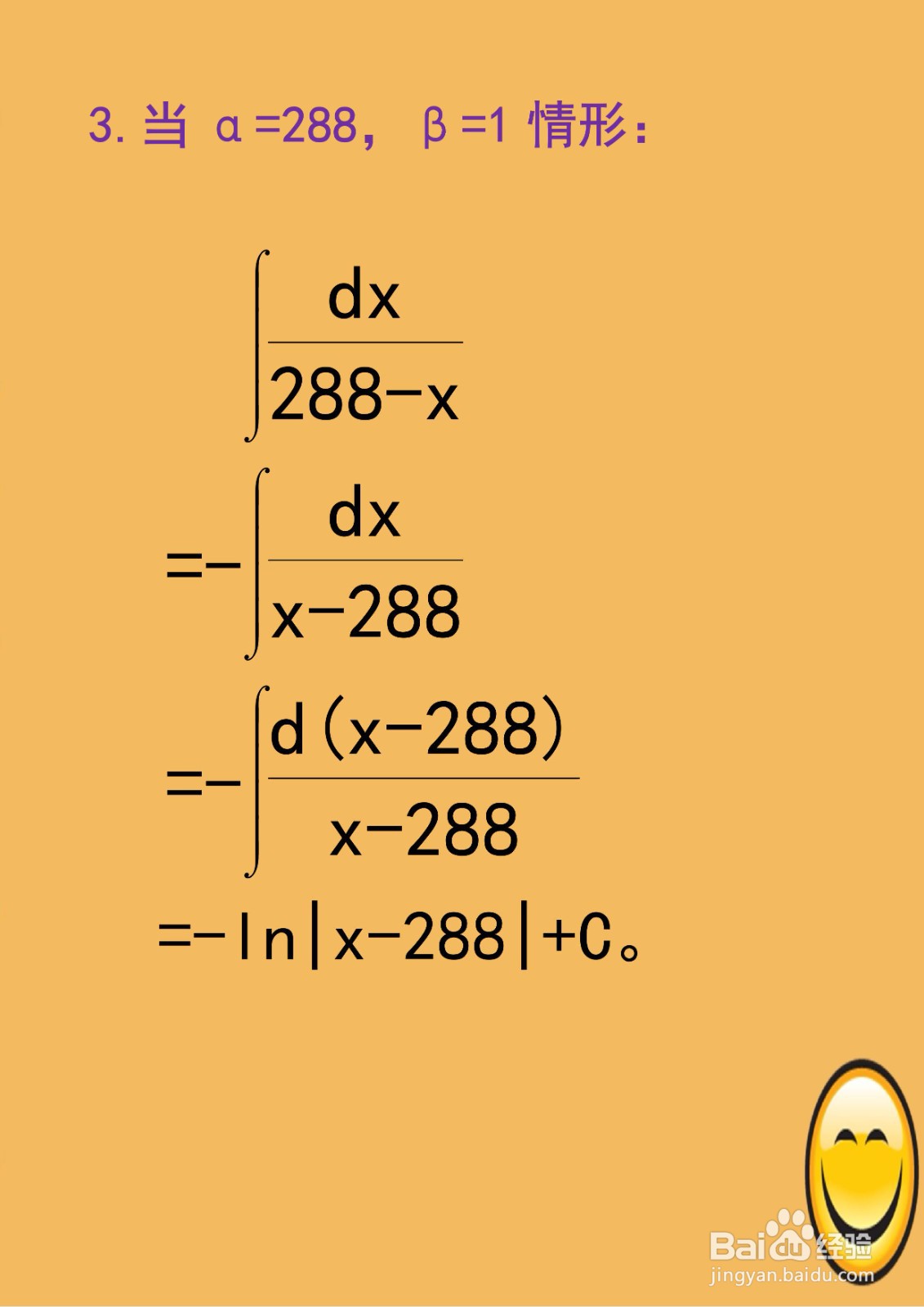[图]5/8

4.当α=180，β=36情形：

∫dx/(180-36x)=-∫dx/(36x-180)

=-(1/36)∫d36x/(36x-180)

=-(1/36)∫d(36x-180)/(36x-180)

=-(1/36)ln|36x-180|+C。

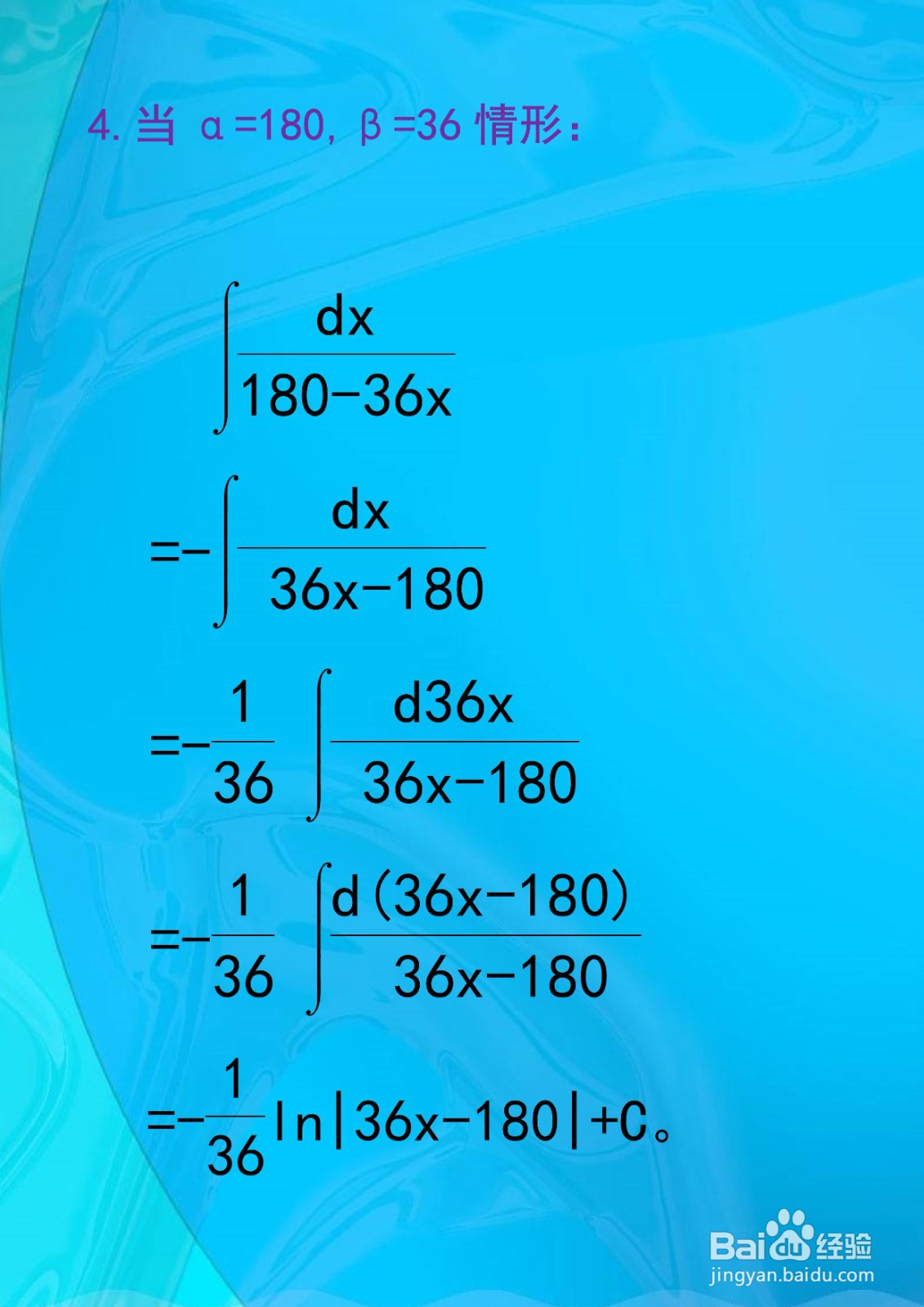[图]6/8

当两个系数均为根式情形

1.当α=√186，β=√206情形：

∫dx/(√186-√206x)=-∫dx/(√206x-√186)

=-(1/√206)∫d√206x/(√206x-√186)

=-(1/√206)∫d(√206x-√186)/(√206x-√186)

=-(1/√206)ln|√206x-√186|+C。

[图]7/8

2.当α=√3275，β=√1020情形：

∫dx/(√3275-√1020x)=-∫dx/(2√255x-5√131)

=-(1/2√255)∫d2√255x/(√206x-5√131)

=-(1/2√255)∫d(2√255x-5√131)/(2√255x-5√131))

=-(1/2√255)ln|2√255x-5√131|+C。

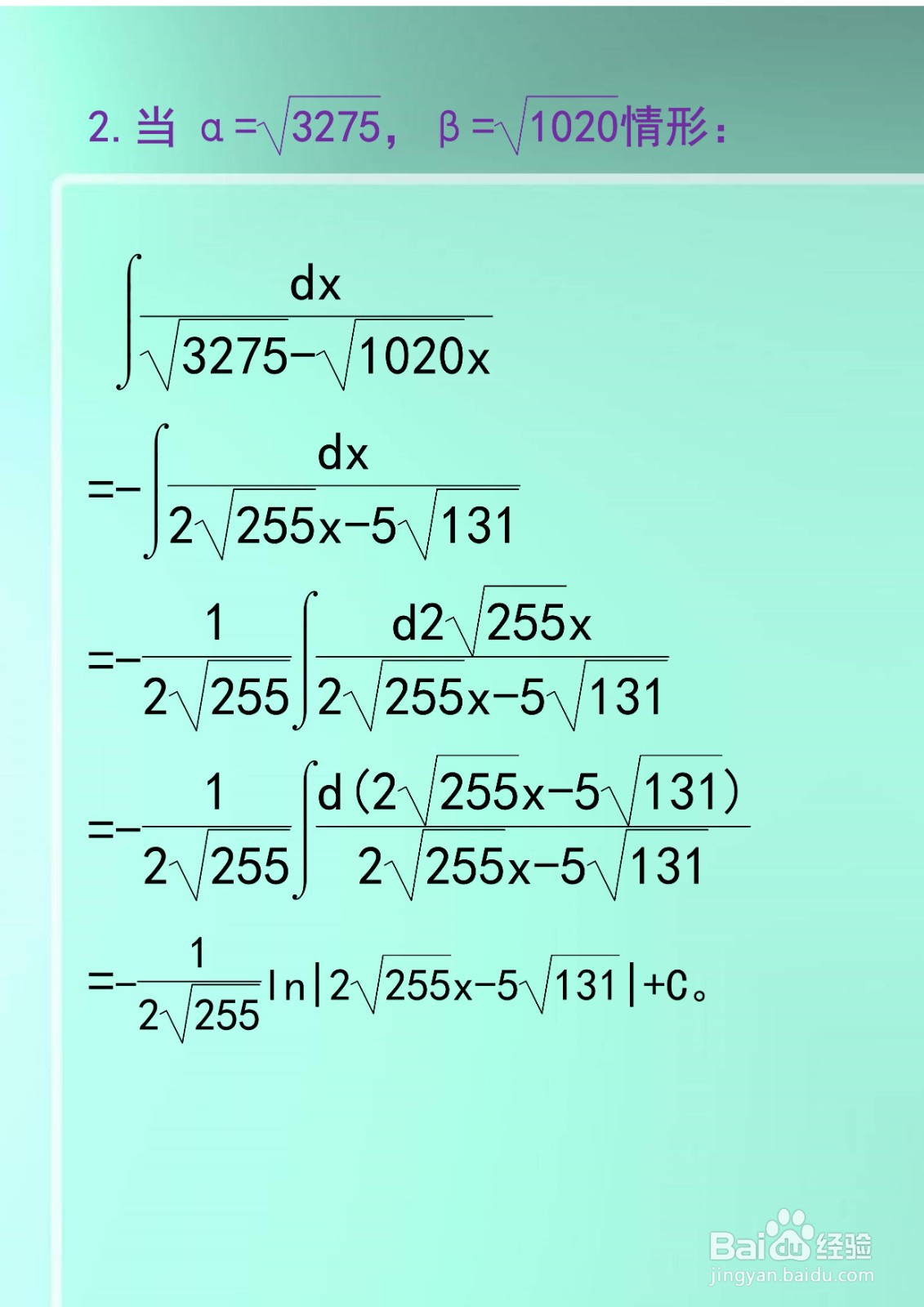[图]8/8

当系数均为分数情况：

当α=2/37√3275，β=5/73情形：

∫dx/(2/37-5x/73)

=-∫dx/(5x/73-2/37)

=-(73/5)∫d(5x/73)/(5x/73-2/37)

=-(73/5)∫d(5x/73-2/37)/(5x/73-2/37)

=-(73/5)ln|5x/73-2/37|+C。

[图]

编辑于2025-06-28，内容仅供参考并受版权保护