函数y=3√(3x^2

来自微信https://weixin.qq.com/的优秀用户吉禄学阁，于2025-06-30在生活百科知识平台总结分享了一篇关于“函数y=3√(3x^2-4)^2的图像示意图迈锐宝”的经验，非常感谢吉禄学阁的辛苦付出，他总结的解决技巧方法及常用办法如下：

本经验通过函数的定义域、单调性、凸凹性、极限等，介绍函数y=3√(3x^2-4)^2的图像的主要步骤。

方法/步骤

1/10分步阅读

根据函数的特征，函数为根式，要求根式内部为非负数，即可解析函数的定义域。

[图]2/10

设A，B是两个非空的数集，如果按某个确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f(x)和它对应，那么就称f:A--B为集合A到集合B的一个函数，记作y=f(x)，x属于集合A。其中，x叫作自变量，x的取值范围A叫作函数的定义域。

3/10

计算函数的一阶导数，进一步即可求出函数的驻点，根据驻点符号，求出函数的单调区间。

[图]4/10

函数的单调性是函数的重要性质，反映了随着自变量的增加函数值的变化趋势，它是研究函数性质的有力工具，在解决比较大小、解决函数图像、值域、最值、不等式问题都有很重要的作用。

5/10

解析函数的凸凹性：求出函数二阶导数，得到函数的拐点，进一步即可求出函数的凸凹区间。

[图]6/10

二阶导数，是原函数导数的导数，将原函数进行二次求导。一般的，函数y=f(x)的导数y'=f'(x)仍然是x的函数，则y'=f'(x)的导数叫作函数y=f(x)的二阶导数。

7/10

函数的极限计算，解析函数在无穷远处的极限。

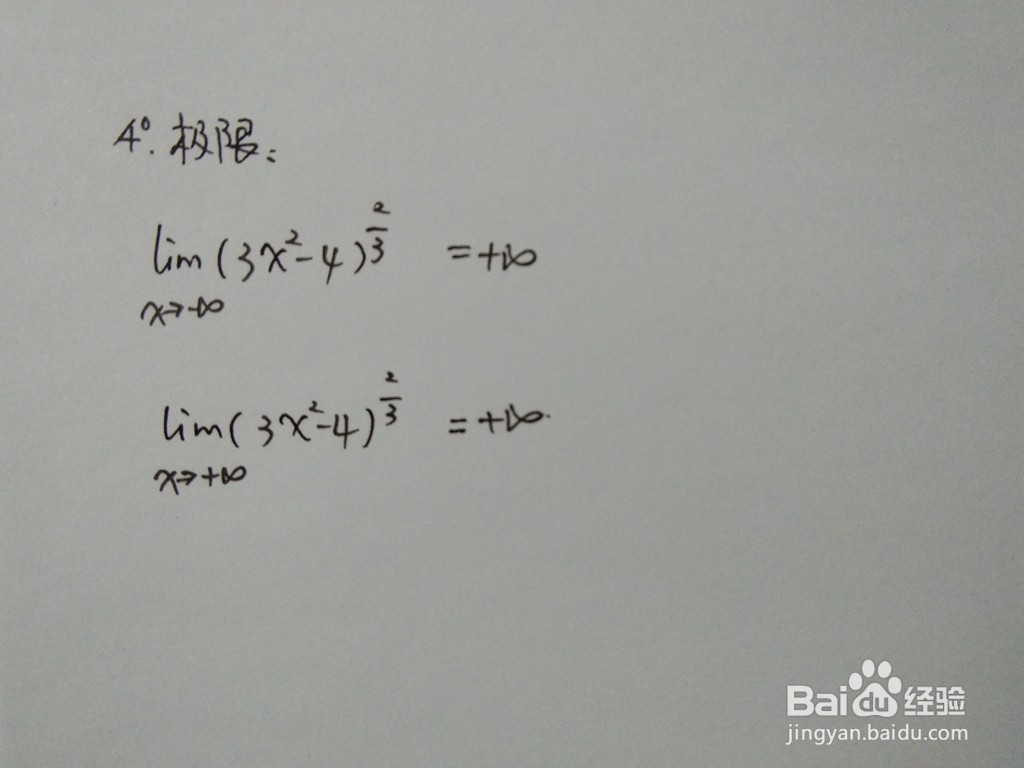[图]8/10

函数上部分特征点列举如下图所示。

[图]9/10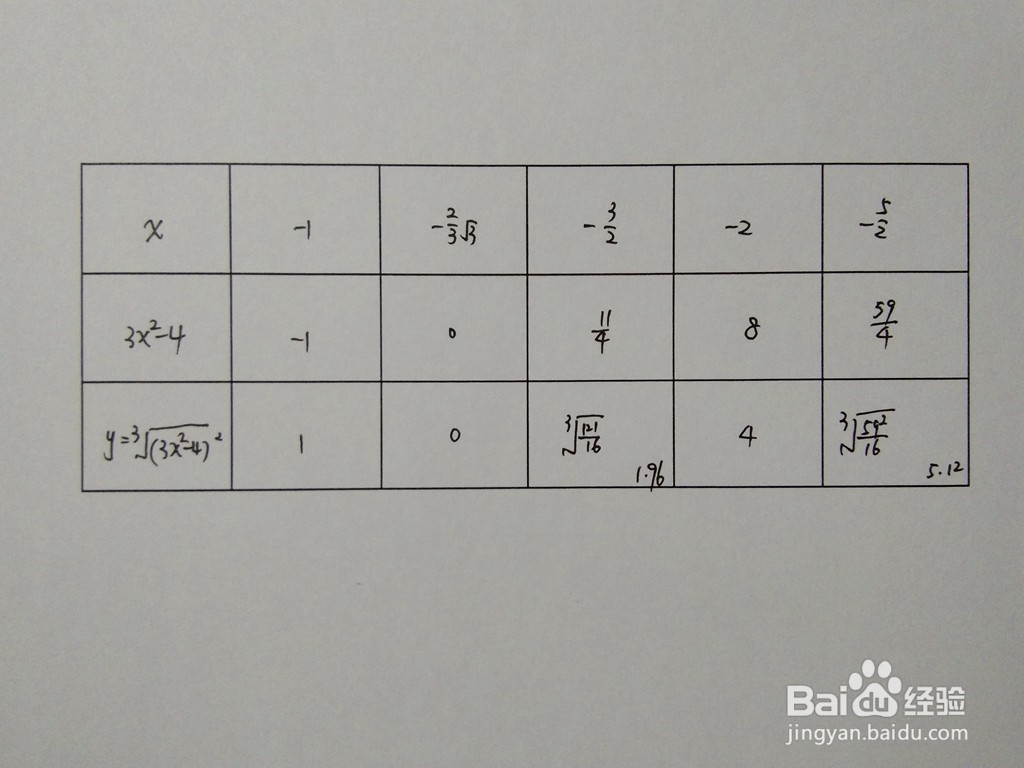[图]10/10

根据函数的的定义域、单调性、凸凹性及极限等性质，即可简要画出函数的图像示意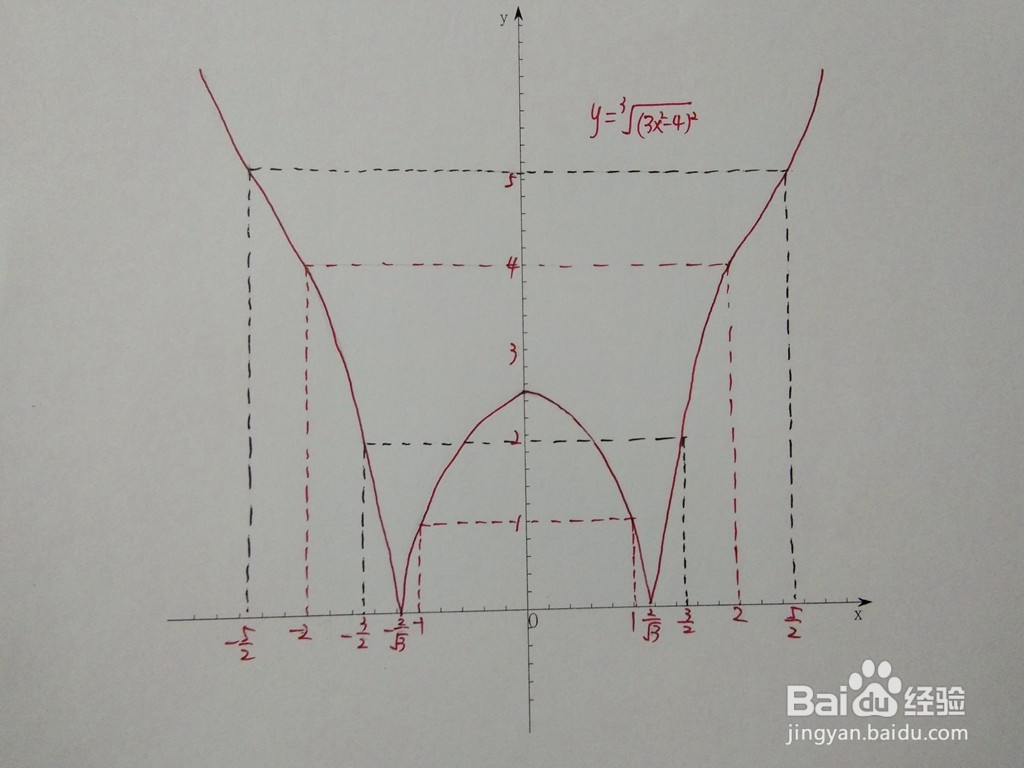图。

[图]

编辑于2025-06-30，内容仅供参考并受版权保护