初中数学七年级下学期数学典型习题及答案解析A3

来自新浪体育http://sports.sina.com.cn/的优秀用户吉禄学阁，于2025-04-14在生活百科知识平台总结分享了一篇关于“初中数学七年级下学期数学典型习题及答案解析A3奥迪q5”的经验，非常感谢吉禄学阁的辛苦付出，他总结的解决技巧方法及常用办法如下：

本经验以3道选择题、3道填空题和4道简答题，详解介绍七年级下学期数学习题解答思路及详细过程步骤。

方法/步骤

1/10分步阅读

1.在平面坐标系中，点N(-47,82)位于( ).

A.第一象限 B.第二象限 C.第三象限 D.第四象限

[图]2/10

2.估算84+√26在哪两个整数之间( ).

A. 4和5 B. 5和6 C. 85和86 D. 89和90

3.如图所示，AB∥CD,AD⊥AC，若∠1=74°，则∠2=( ).

A.16° B. 84° C. 69° D. 74°

[图]3/10

֍.填空题：1.计算√1296的平方根= .

解析：本题考察的主要是平方根知识，一个正数如果有平方根，那么必定有两个，它们互为相反数。显然，如果知道了这两个平方根的一个，那么就可以及时的根据相反数的概念得到它的另一个平方根。

本题√1296=36，所以：36的平方根=±6.

֍.填空题：2.若p和q为实数，且√(p+102)+(q-111)²=0，则(p-q)/28= .

解析：本题考察的是两个非负数和为0的相关知识，则这两个数必须同时为0。本题中√(p+102)≥0，(q-111)²≥0，又二者的和为0，所以有：

p+102=0且q-111=0，所以：

p=-102, q=111,代入所求式有：

代数式=(p-q)/28=(-102-111)/28=-213/28,为本题所求值。

[图]4/10

֍.填空题：3.长方形ABCD的边AB=30,BC=24，若将该长方形放在平面直角坐标系中，使点A的坐标为(-2, 5)，且AB∥x轴，则点C的坐标为： .

解析：本题是考察直角坐标系点的坐标有关知识。对于本题由于仅仅告诉AB和BC的长，但点的位置不明确，因此在坐标系中会有几种情况，具体如下：

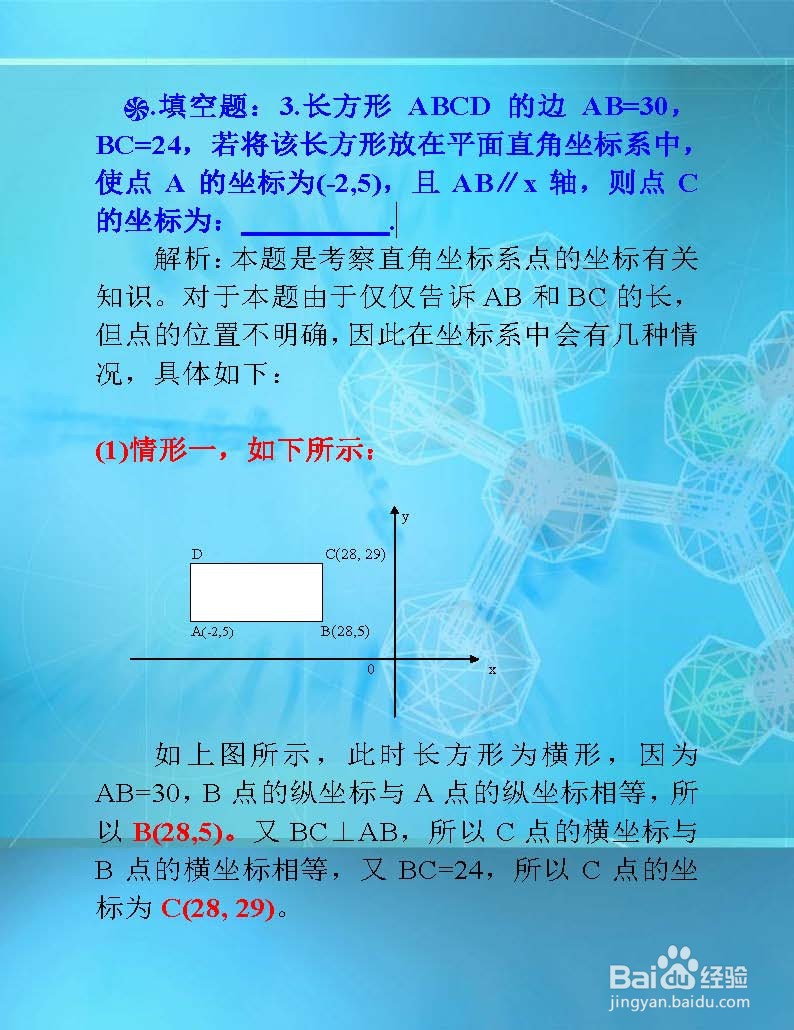
(1)情形一，如下所示：

如上图所示，此时长方形为横形，因为AB=30，B点的纵坐标与A点的纵坐标相等，所以B(28,5)。又BC⊥AB，所以C点的横坐标与B点的横坐标相等，又BC=24，所以C点的坐标为C(28, 29)。

[图]5/10

(2)情形二，如下所示：

如上图所示，此时长方形为横形，因为AB=30，B点的纵坐标与A点的纵坐标相等，所以B(-32, 5)。又BC⊥AB，所以C点的横坐标与B点的横坐标相等，又BC=24，所以C点的坐标为C(-32,29)。

(3)情形三，如下所示：

如上图所示，长方形为横形，因为AB=30，B点的横坐标与A点的横坐标相等，所以B(-32,5)。又BC⊥AB，所以C点的纵坐标与B点的纵坐标相等，又BC=24，所以C点的坐标为C(-32,-19)。

[图]6/10

(4)情形四，如下所示：

如上图所示，长方形为横形，因为AB=30，B点的横坐标与A点的横坐标相等，所以B(28,5)。又BC⊥AB，所以C点的纵坐标与B点的纵坐标相等，又BC=24，所以C点的坐标为C(28,-19)。

[图]7/10

֍.简答题：1.代入法计算方程组y=3x+20,36x+5y=74的解。

解：将方程y=3x+20代入后续方程有：

36x+5*(3x+20)=74,

即:36x+15x+100=74,

51x=-26,则x=-26/51.

再代入方程有：y=-26/51*3+20=314/17,

所以方程的解为：x=-26/51，y=314/17。

֍.简答题：2.加减法计算方程组35x+11y=40,35x-31y=-38的解。

解：将上述两个方程相减，有：

11y+31y=40+38,即：

42y=78,所以y=13/7.

代入其中一个方程有：

35x+11*13/7=40，

35x=137/7,

所以x=137/245，即方程的解为：

x=137/245，y=13/7。

[图]8/10

֍.简答题：3.解不等式(21-x)/13-31x＜8-(x+24)/14.

解：将不等式进行变化，方程两边同时乘以182，有：

14(21-x)-14*31x＜13*8-13*(x+24),

294-14x-434x＜104-13x-312,

294+312-104＜(14+434-13)x,

即：435x＞502，

则：x>502/435.

故不等式的解集为：{x| x>502/435,x∈R}.

[图]9/10

֍.简答题：4.如下图所示，在平面直角坐标系中，点A,B的坐标分别为A(x,0)，B(b,0),且x,y满足|x+15|+√(y-23)=0，点C的坐标为(0, 16)。

(1)求x,y的值及S△ABC;

(2)若点M在x轴上，且S△ACM=(1/3)S△ABC，试求点M的坐标。

(1)求x,y的值及S△ABC;

解：根据|x+15|+√(y-23)=0的特征有：

|x+15|≥0，√(y-23)≥0，又因为二者的和为0，

即：x+15=0且y-23=0,

所以：x=-15，y=23.

在△ABC中，有：

AB=y-x=23-(-15)=23+15=38.

三角形的高h=16,

所以：S△ABC=(1/2)*AB*h

=(1/2)*38*16

=304平方单位。

[图]10/10

(2)若点M在x轴上，且S△ACM=(1/3)S△ABC，试求点M的坐标。

解：设M(m,0),对于△ACM与△ABC有：

底边分别为AM和AB，C点到这两个底边的高相等，

又S△ACM=(1/3)S△ABC，

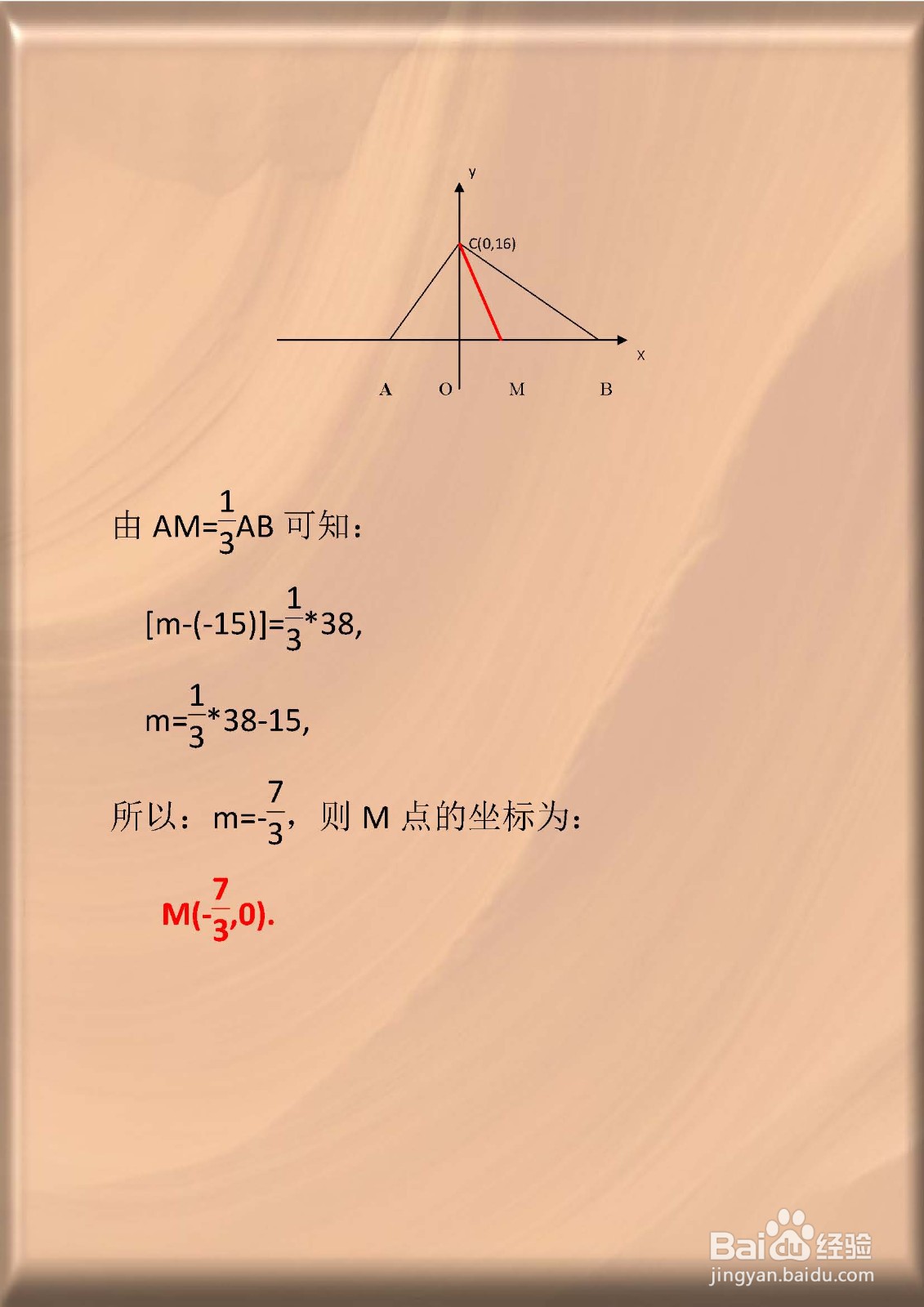
所以：AM=(1/3)*AB.

即：[m-(-15)]= (1/3)*38,

m=(1/3)*38-15,

所以：m=-7/3，

则M点的坐标为：M(-7/3,0).

[图]

编辑于2025-04-14，内容仅供参考并受版权保护