函数y=5x/(6+x^2)的图像示意图

来自新浪财经https://finance.sina.com.cn/的优秀用户吉禄学阁，于2025-05-06在生活百科知识平台总结分享了一篇关于“函数y=5x/(6+x^2)的图像示意图英雄儿女”的经验，非常感谢吉禄学阁的辛苦付出，他总结的解决技巧方法及常用办法如下：

本经验通过函数的定义域、单调性、凸凹性、极限、奇偶等性质，介绍函数用导数工具画函数y=5x/(3+x^2)的图像的主要步骤。

主要方法与步骤

1/9分步阅读

函数分母不为0，即可解析函数自变量可以取全体实数，所以函数y=5x/(3+x^2)的定义域为：（-∞，+∞）。

[图]2/9

定义域是指该函数的有效范围，函数的定义域就是使得这个函数关系式有意义的实数的全体构成的集合。

3/9

函数y=5x/(3+x^2)的单调性也叫函数的增减性。当函数 f(x) 的自变量在其定义区间内增大(或减小)时，函数值f(x)也随着增大(或减小)，则称该函数为在该区间上具有单调性。

[图]4/9

计算函数y=5x/(3+x^2)的二阶导数，进一步解析函数的拐点，从而解析函数y=5x/(3+x^2)的凸凹性和凸凹区间。

[图]5/9

根据函数y=5x/(3+x^2)特征，函数分母为偶函数，分子为奇函数，所以整体函数y=5x/(3+x^2)为奇函数。

[图]6/9

在数学中，一个函数f(x) 被称为奇函数，当且仅当对于任意实数x，都有f(-x)=-f(x)成立；而一个函数f(x)f(x)被称为偶函数，当且仅当对于任意实数 x，都有f(-x)=f(x) 成立。

判断一个函数的奇偶性可以通过代入-x并进行比较的方法进行。具体来说：

对于奇函数f(x)，我们有f(-x)=-f(x)，因此f(-x)+f(x)=0。

对于偶函数f(x)，我们有f(-x)=f(x)，因此f(-x)-f(x)=0。

7/9

结合函数y=5x/(3+x^2)的单调性，求出函数y=5x/(3+x^2)在无穷大处的极限。

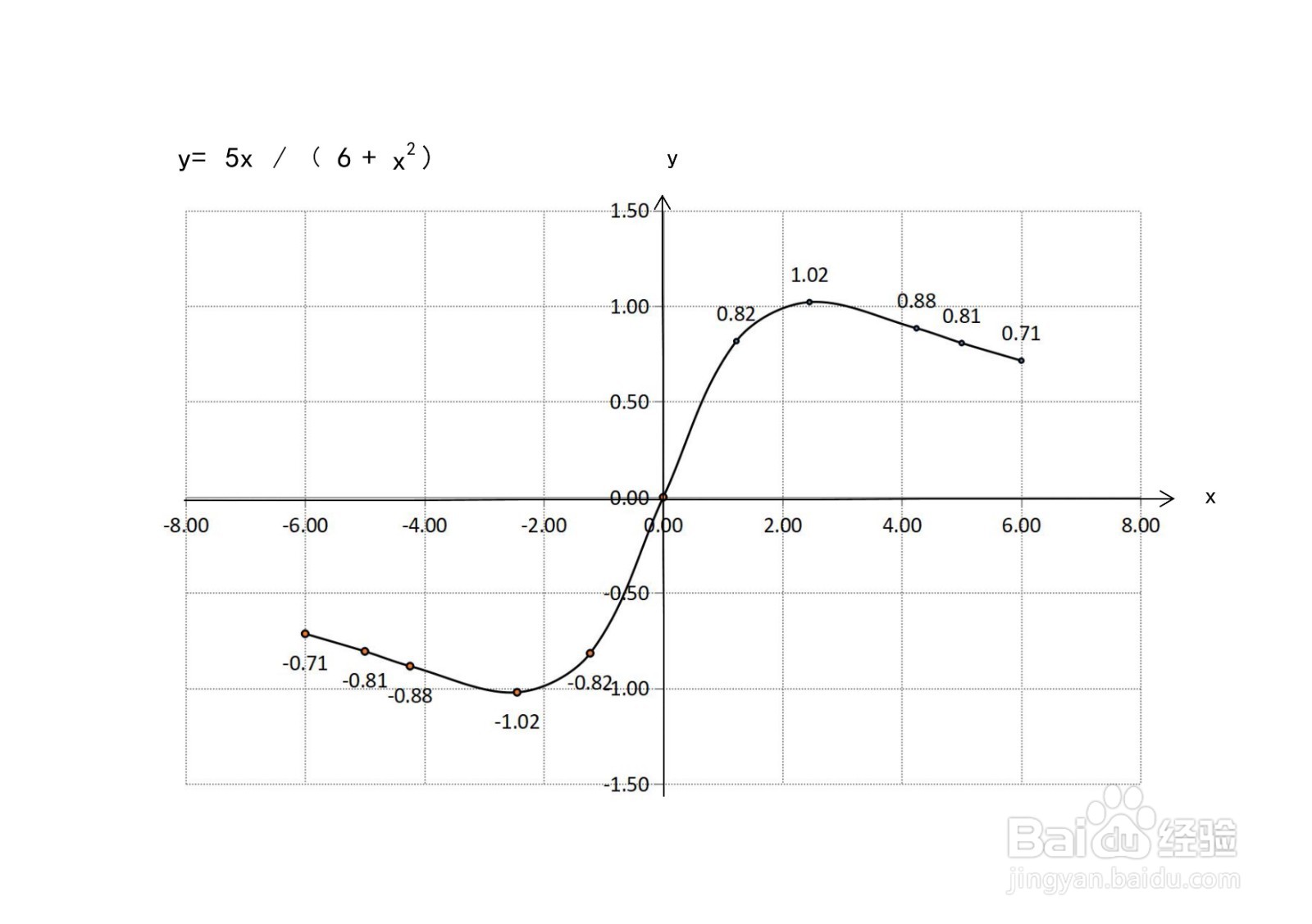
[图]8/9

函数y=5x/(3+x^2)上的五点图表列举如下：

[图]9/9

根据函数的定义域、值域、单调性、凸凹性、奇偶性以及极限等性质，以及函数的单调区间、凸凹区间，可画出函数y=5x/(3+x^2)的示意图。

[图]

编辑于2025-05-06，内容仅供参考并受版权保护